Bayesian Neural Network¶

Usually, neural networks are optimized in order to get a fixed value for the weights and biases which allow the model perform a specific task successfully. In a Bayesian neural network the weights and biases are distributed rather than fixed. This type of model could be treated as an ensemble of many neural networks, train using a Bayesian inference.

Using a Bayesian approach for the neural network training allows the analyzer to estimate the uncertainty and to make the decision of the model more robust against the input data.

Difference between usual NN and BNN¶

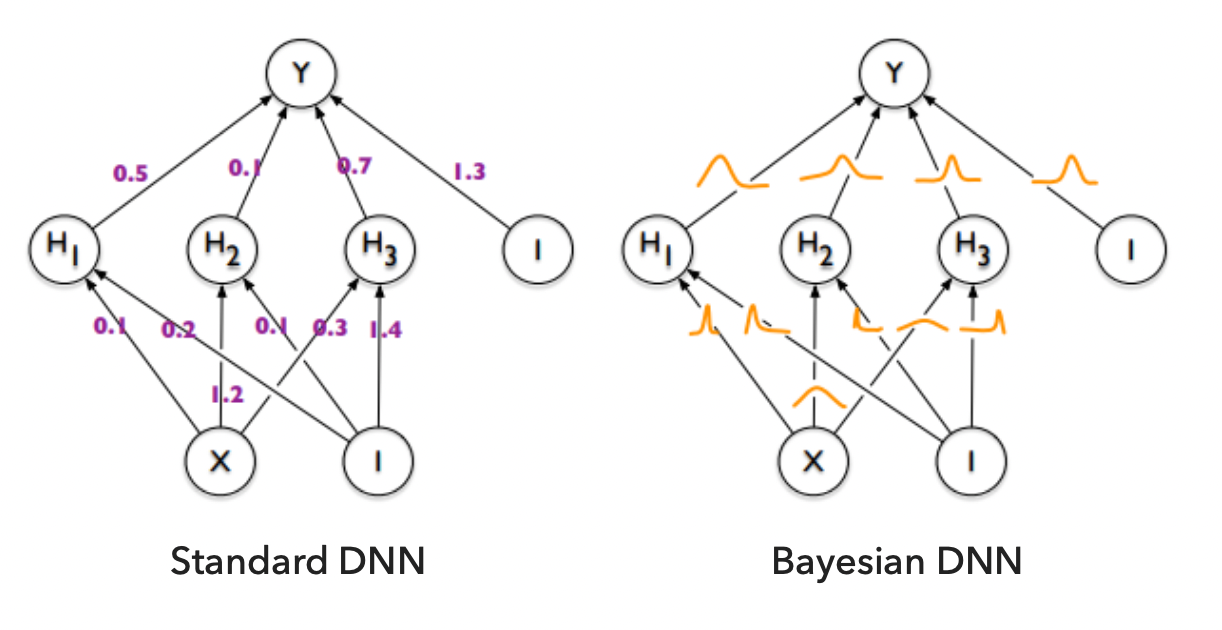
Placeholder

Training of NN and BNN¶

NNBNN

Placeholder The parameters $\theta$ are optimized in order to minimaze the loss function.

Placeholder The process is to learn the probability distributions for weights and biases that maximize the likelihood of getting a high probability for the correct data/label $D(x,y)$ pairs. The parameters of the weight distributions -- mean and standard deviation -- are the results of the loss function optimization.

Training Procedure¶

1. Introduce the prior distribution over model parameter w
2. Compute posterio p(w|D) using Bayesian rule
3. Take the average over the posterior distribution

Prediction of NN and BNN¶

NNBNN

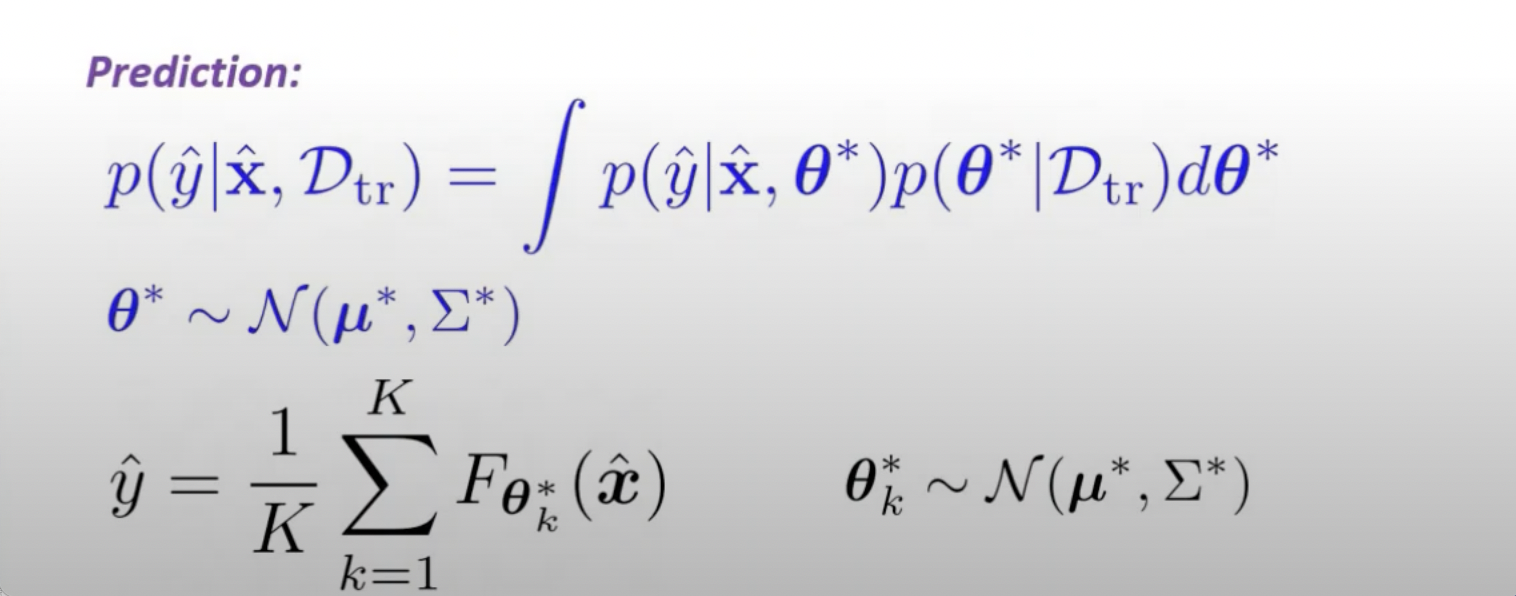
Placeholder

Uncertainty¶

There are two types of BNN uncertainties:

AlletonicEpistemic

Alletonic - uncertainties due to the lack of knowledge, comes from data or enviroment $p (\theta|D)$

Epistemic - uncertainties of the model parameter $p(y|x,\theta)$

Packages¶

Here we will list a few of the machine learning packages which can be used to develop a probabilistic neural network.

TensorflowPyro

    pip install --upgrade tensorflow-probability

    pip install pyro

Modules Description:¶

Distribution and sampling¶

TensorflowPyro

Distribution and sampling¶

TensorflowPyro

Example¶

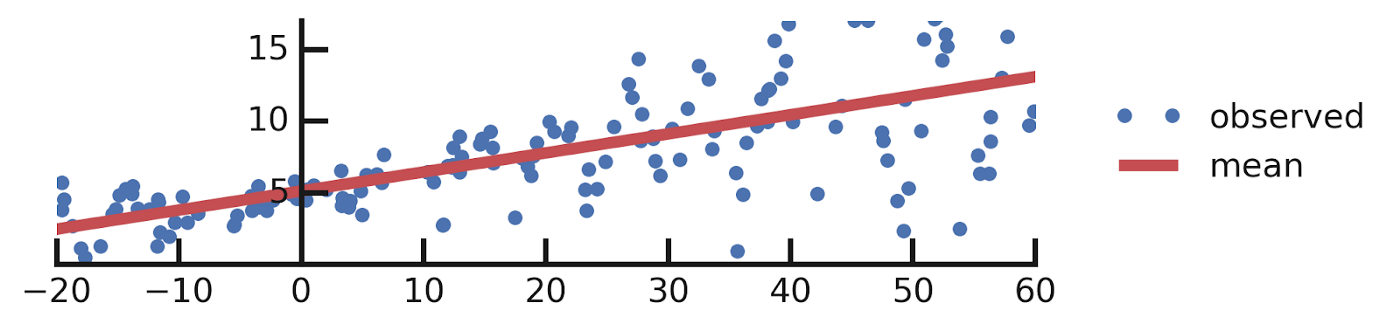
Let's consider simple linear regression as an example and compare it to the Bayesian analog.

Lets consider simple dataset D(x, y) and we want to fit some linear function: y=ax+b+e, where a,b are learnable parameters and e is observation noise.

Synthetic datasettensorflow_probabilitypyro

import numpy as np
w0 = 0.125
b0 = 5.
x_range = [-20, 60]

def load_dataset(n=150, n_tst=150):
    np.random.seed(43)
    def s(x):
        g = (x - x_range[0]) / (x_range[1] - x_range[0])
        return 3 * (0.25 + g**2.)
    x = (x_range[1] - x_range[0]) * np.random.rand(n) + x_range[0]
    eps = np.random.randn(n) * s(x)
    y = (w0 * x * (1. + np.sin(x)) + b0) + eps
    x = x[..., np.newaxis]
    x_tst = np.linspace(*x_range, num=n_tst).astype(np.float32)
    x_tst = x_tst[..., np.newaxis]
    return y, x, x_tst

y, x, x_tst = load_dataset()

Let's consider you write your network model in a single tf.function.

import tensorflow as tf
import tensorflow_probability as tfp
tfd = tfp.distributions

# Build model.
model = tf.keras.Sequential([
tf.keras.layers.Dense(1),
tfp.layers.DistributionLambda(lambda t: tfd.Normal(loc=t, scale=1)),
])

# Define the loss:
negloglik = lambda y, rv_y: -rv_y.log_prob(y)

# Do inference.
model.compile(optimizer=tf.optimizers.Adam(learning_rate=0.05), loss=negloglik)
model.fit(x, y, epochs=500, verbose=False)

# Make predictions.
yhat = model(x_tst)

# coding: utf-8

from pyro.nn import PyroSample

# Specify model.

class BayesianRegression(PyroModule):
    def __init__(self, in_features, out_features):
        super().__init__()
        self.linear = PyroModule[nn.Linear](in_features, out_features)
        self.linear.weight = PyroSample(dist.Normal(0., 1.).expand([out_features, in_features]).to_event(2))
        self.linear.bias = PyroSample(dist.Normal(0., 10.).expand([out_features]).to_event(1))

    def forward(self, x, y=None):
        sigma = pyro.sample("sigma", dist.Uniform(0., 10.))
        mean = self.linear(x).squeeze(-1)
        with pyro.plate("data", x.shape[0]):
            obs = pyro.sample("obs", dist.Normal(mean, sigma), obs=y)
        return mean



# Build model.
model = BayesianRegression()

# Fit model given data.
coeffs, linear_response, is_converged, num_iter = tfp.glm.fit(
model_matrix=features[:, tf.newaxis],
response=tf.cast(labels, dtype=tf.float32),
model=model)
# ==> coeffs is approximately [1.618] (We're golden!)

# Do inference.
model.compile(optimizer=tf.optimizers.Adam(learning_rate=0.01), loss=negloglik)
model.fit(x, y, epochs=1000, verbose=False);

# Profit.
[print(np.squeeze(w.numpy())) for w in model.weights];
yhat = model(x_tst)
assert isinstance(yhat, tfd.Distribution)

The output of the model:

Placeholder

Variational Autoencoder¶

Generative models can be built using a Bayesian neural network. The variational autoencoder is one popular way to forma generative model.

Let's consider the example of generating the images:

The generating process consist of two steps:

Sampling the latent variable from prior distribution
Drawing the sample from stochastic process $x-p(z|x)$

Objective:

$p(z)$ the prior on the latent representation $z$ , $q(z|x)$ , the variational encoder, and $p(x|z)$ , the decoder — how likely is the image x given the latent representation z.

Loss¶

Once we define the procedure for the generation process the objective function should be chosen for the optimization process. In order to train the network, we maximize the ELBO (Evidence Lower Bound) objective.

Prior¶

p(z), the prior on the latent representation z,

q(z|x), the variational encoder, and

p(x|z), the decoder — how likely is the image x given the latent representation z.

Encoder and Decoder¶

tensorflowpyro

Training¶

tensorflowpyro

Results¶

tensorflowpyro

Normalizing Flows¶

Defition¶

tensorflowpyro

Training¶

tensorflowpyro

Inference¶

tensorflowpyro

Resources¶

Bayesian NN¶

1. https://arxiv.org/pdf/2007.06823.pdf
2. http://krasserm.github.io/2019/03/14/bayesian-neural-networks/
3. https://arxiv.org/pdf/1807.02811.pdf

Normalizing Flow:¶

1. https://arxiv.org/abs/1908.09257
2. https://arxiv.org/pdf/1505.05770.pdf

Variational AutoEncoder:¶

1. https://arxiv.org/abs/1312.6114
2. https://pyro.ai/examples/vae.html
3. https://www.tensorflow.org/probability/examples/Probabilistic_Layers_VAE