Skip to content

Data augmentation

Introduction

This introduction is based on papers by Shorten & Khoshgoftaar, 2019 and Rebuffi et al., 2021 among others

With the increasing complexity and sizes of neural networks one needs huge amounts of data in order to train a state-of-the-art model. However, generating this data is often very resource and time intensive. Thus, one might either augment the existing data with more descriptive variables or combat the data scarcity problem by artificially increasing the size of the dataset by adding new instances without the resource-heavy generation process. Both processes are known in machine learning (ML) applications as data augmentation (DA) methods.

The first type of these methods is more widely known as feature generation or feature engineering and is done on instance level. Feature engineering focuses on crafting informative input features for the algorithm, often inspired or derived from first principles specific to the algorithm's application domain.

The second type of method is done on the dataset level. These types of techniques can generally be divided into two main categories: real data augmentation (RDA) and synthetic data augmentation (SDA). As the name suggests, RDA makes minor changes to the already existing data in order to generate new samples, whereas SDA generates new data from scratch. Examples of RDA include rotating (especially useful if we expect the event to be rotationally symmetric) and zooming, among a plethora of other methods detailed in this overview article. Examples of SDA include traditional sampling methods and more complex generative models like Generative Adversaial Netoworks (GANs) and Variational Autoencoders (VAE). Going further, the generative methods used for synthetic data augmentation could also be used in fast simulation, which is a notable bottleneck in the overall physics analysis workflow.

Dataset augmentation may lead to more successful algorithm outcomes. For example, introducing noise into data to form additional data points improves the learning ability of several models which otherwise performed relatively poorly, as shown by Freer & Yang, 2020. This finding implies that this form of DA creates variations that the model may see in the real world. If done right, preprocessing the data with DA will result in superior training outcomes. This improvement in performance is due to the fact that DA methods act as a regularizer, reducing overfitting during training. In addition to simulating real-world variations, DA methods can also even out categorical data with imbalanced classes.

Data Augmentation
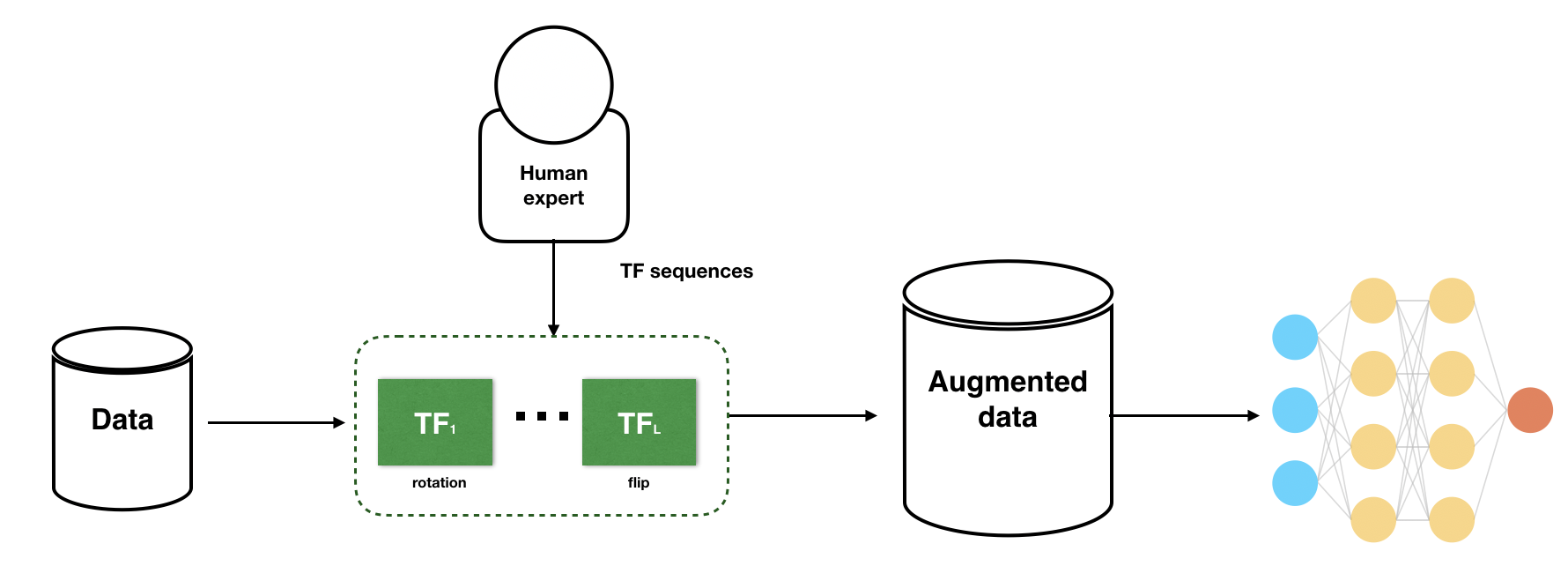Fig. 1: Generic pipeline of a heuristic DA (figure taken from Li, 2020)

Before diving more in depth into the various DA methods and applications in HEP, here is a list of the most notable benefits of using DA methods in your ML workflow:

  • Improvement of model prediction precision
  • More training data for the model
  • Preventing data scarcity for state-of-the-art models
  • Reduction of over overfitting and creation of data variability
  • Increased model generalization properties
  • Help in resolving class imbalance problems in datasets
  • Reduced cost of data collection and labeling
  • Enabling rare event prediction

And some words of caution:

  • There is no 'one size fits all' in DA. Each dataset and usecase should be considered separately.
  • Don't trust the augmented data blindly
  • Make sure that the augmented data is representative of the problem at hand, otherwise it will negatively affect the model performance.
  • There must be no unnecessary duplication of existing data, only by adding unique information we gain more insights.
  • Ensure the validity of the augmented data before using it in ML models.
  • If a real dataset contains biases, data augmented from it will contain biases, too. So, identification of optimal data augmentation strategy is important. So, double check your DA strategy.

Feature Engineering

This part is based mostly on Erdmann et al., 2018

Feature engineering (FE) is one of the key components of a machine learning workflow. This process transforms and augments training data with additional features in order to make the training more effective.

With multi-variate analyeses (MVAs), such boosted decision trees (BDTs) and neural networks, one could start with raw, "low-level" features, like four-momenta, and the algorithm can learn higher level patterns, correlations, metrics, etc. However, using "high-level" variables, in many cases, leads to outcomes superior to the use of low-level variables. As such, features used in MVAs are handcrafted from physics first principles.

Still, it is shown that a deep neural network (DNN) can perform better if it is trained with both specifically constructed variables and low-level variables. This observation suggests that the network extracts additional information from the training data.

HEP Application - Lorentz Boosted Network

For the purposeses of FE in HEP, a novel ML architecture called a Lorentz Boost Network (LBN) (see Fig. 2) was proposed and implemented by Erdmann et al., 2018. It is a multipurpose method that uses Lorentz transformations to exploit and uncover structures in particle collision events. LBN is the first stage of a two-stage neural network (NN) model, that enables a fully autonomous and comprehensive characterization of collision events by exploiting exclusively the four-momenta of the final-state particles.

Within LBN, particles are combined to create rest frames representions, which enables the formation of further composite particles. These combinations are realized via linear combinations of N input four-vectors to a number of M particles and rest frames. Subsequently these composite particles are then transformed into said rest frames by Lorentz transformations in an efficient and fully vectorized implementation.

The properties of the composite, transformed particles are compiled in the form of characteristic variables like masses, angles, etc. that serve as input for a subsequent network - the second stage, which has to be configured for a specific analysis task, like classification.

The authors observed leading performance with the LBN and demonstrated that LBN forms physically meaningful particle combinations and generates suitable characteristic variables.

The usual ML workflow, employing LBN, is as follows:

Step-1: LBN(M, F)

    1.0: Input hyperparameters: number of combinations M; number of features F
    1.0: Choose: number of incoming particles, N, according to the research
         question

    1.1: Combination of input four-vectors to particles and rest frames

    1.2: Lorentz transformations

    1.3 Extraction of suitable high-level objects


Step-2: NN

    2.X: Train some form of a NN using an objective function that depends on
         the analysis / research question.
LBN
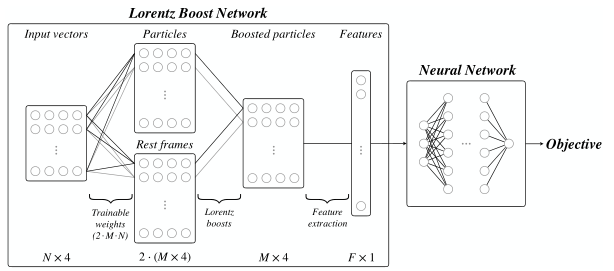Fig. 2: The Lorentz Boost Network architecture (figure taken from Erdmann et al., 2018)

The LBN package is also pip-installable:

pip install lbn

RDA Techniques

This section and the following subsection are based on the papers by Freer & Yang, 2020, Dolan & Ore, 2021, Barnard et al., 2016, and Bradshaw et al., 2019

RDA methods augment the existing dataset by performance some transformation on the existing data points. These transformations could include rotation, flipping, color shift (for an image), Fourier transforming (for signal processing) or some other transformation that preserves the validity of the data point and its corresponding label. As mentioned in Freer & Yang, 2020, these types of transformations augment the dataset to capture potential variations that the population of data may exhibit, allowing the network to capture a more generalized view of the sampled data.

HEP Application - Zooming

In Barnard et al., 2016, the authors investigate the effect of parton shower modelling in DNN jet taggers using images of hadronically decaying W bosons. They introduce a method known as zooming to study the scale invariance of these networks. This is the RDA strategy used by Dolan & Ore, 2021. Zooming is similar to a normalization procedure such that it standardizes features in signal data, but it aims to not create similar features in background.

After some standard data processing steps, including jet trimming and clustering via the \(k_t\) algorithm, and some further processing to remove spatial symmetries, the resulting jet image depicts the leading subjet and subleading subjet directly below. Barnard et al., 2016 notes that the separation between the leading and subleading subjets varies linearly as \(2m/p_T\) where \(m\) and \(p_T\) are the mass and transverse momentum of the jet. Standardizing this separation, or removing the linear dependence, would allow the DNN tagger to generalize to a wide range of jet \(p_T\). To this end, the authors construct a factor, \(R/\DeltaR_{act}\), where \(R\) is some fixed value and \(\DeltaR_{act}\) is the separation between the leading and subleading subjets. To discriminate between signal and background images with this factor, the authors enlarge the jet images by a scaling factor of \(\text{max}(R/s,1)\) where \(s = 2m_W/p_T\) and \(R\) is the original jet clustering size. This process of jet image enlargement by a linear mass and \(p_T\) dependent factor to account for the distane between the leading and subleading jet is known as zooming. This process can be thought of as an RDA technique to augment the data in a domain-specific way.

Advantage of using the zooming technique is that it makes the construction of scale invariant taggers easier. Scale invariant searches which are able to interpolate between the boosted and resolved parts of phase space have the advantage of being applicable over a broad range of masses and kinematics, allowing a single search or analysis to be effective where previously more than one may have been necessary.

As predicted the zoomed network outperforms the unzoomed one, particularly at low signal efficiency, where the background rejection rises by around 20%. Zooming has the greatest effect at high pT.

Traditional SDA Techniques

Text in part based on He et al., 2010

Generally speaking, imbalanced learning occurs whenever some type of data distribution dominates the instance space compared to other data distributions. Methods for handling imbalanced learning problems can be divided into the following five major categories:

  • Sampling strategies
  • Synthetic data generation (SMOTE & ADASYN & DataBoost-IM) - aims to overcome the imbalance by artificially generating data samples.
  • Cost-sensitive learning - uses cost-matrix for different types of errors or instance to facilitate learning from imbalanced data sets. This means that cost-sensitive learning does not modify the imbalanced data distribution directly, but targets this problem by using different cost-matrices that describe the cost for misclassifying any particular data sample.
  • Active learning - conventionally used to solve problems related to unlabeled data, though recently it has been used in learning imbalanced data sets. Instead of searching the entire training space, this method effectively selects informative instances from a random set of training populations, therefore significantly reducing the computational cost when dealing with large imbalanced data sets.
  • Kernel-based methods - by integrating the regularized orthogonal weighed least squares (ROWLS) estimator, a kernel classifier construction algorithm is based on orthogonal forward selection (OFS) to optimize the model generalization for learning from two-class imbalanced data sets.

Sampling

When the percentage of the minority class is less than 5%, it can be considered a rare event. When a dataset is imbalanced or when a rare event occurs, it will be difficult to get a meaningful and good predictive model due to lack of information about the rare event Au et al., 2010. In these cases, re-sampling techniques can be helpful. The re-sampling techniques are implemented in four different categories: undersampling the majority class, oversampling the minority class, combining over- and undersampling, and ensembling sampling. Oversampling and undersampling are found to work well in improving the classification for the imbalanced dataset. Yap et al., 2013

Stratified sampling (STS) This technique is used in cases where the data can be partitioned into strata (subpopulations), where each strata should be collectively exhaustive and mutually exclusive. The process of dividing the data into homogeneus subgroups before sampling is referred to as stratification. The two common strategies of STS are proportionate allocation (PA) and optimum (disproportionate) allocation (OA). The former uses a fraction in each of the stata that is proportional to that of the total population. The latter uses the standard deviation of the distribution of the variable as well, so that the larger samples are taken from the strata that has the greatest variability to generate the least possible sampling variance. The advantages of using STS include smaller error in estimation (if measurements within strata have lower standard deviation) and similarity in uncertainties across all strata in case there is high variability in a given strata.

NOTE: STS is only useful if the population can be exhaustively partitioned into subgroups. Also in case of unknown class priors (the ratio of strata to the whole population) might have deleterious effects on the classification performance.

Over- and undersampling Oversampling randomly duplicates minority class samples, while undersampling discards majority class samples in order to modify the class distribution. While oversampling might lead to overfitting, since it makes exact copies of the minority samples, undersampling may discard potentially useful majority samples.

Oversampling and undersampling are essentially opposite and roughly equivalent techniques. There are also more complex oversampling techniques, including the creation of artificial data points with algorithms like Synthetic Minority Over-sampling TEchnique (SMOTE).

It has been shown that the combination of SMOTE and undersampling performs better than only undersampling the majority class. However, over- and undersampling remain popular as it each is much easier to implement alone than in some complex hybrid approach.

Synthetic Minority Over-sampling Technique (SMOTE) Text mostly based on Chawla et al., 2002 and in part on He et al., 2010

In case of Synthetic Minority Over-sampling Technique (SMOTE), the minority class is oversampled by creating synthetic examples along the line segments joining any or all of the \(k\)-nearest neighbours in the minority class. The synthetic examples cause the classifier to create larger and less specific decision regions, rather than smaller and more specific regions. More general regions are now learned for the minority class samples rather than those being subsumed by the majority class samples around them. In this way SMOTE shifts the classifier learning bias toward the minority class and thus has the effect of allowing the model to generalize better.

There also exist extensions of this work like SMOTE-Boost in which the syntetic procedure was integrated with adaptive boosting techniques to change the method of updating weights to better compensate for skewed distributions.

So in general SMOTE proceeds as follows 

SMOTE(N, X, k)
Input: N - Number of synthetic samples to be generated
       X - Underrepresented data
       k - Hyperparameter of number of nearest neighbours to be chosen

Create an empty list SYNTHETIC_SAMPLES
While N_SYNTHETIC_SAMPLES < N
    1. Randomly choose an entry xRand from X
    2. Find k nearest neighbours from X
    3. Randomly choose an entry xNeighbour from the k nearest neighbours
    4. Take difference dx between the xRand and xNeighbour
    5. Multiply dx by a random number between 0 and 1
    6. Append the result to SYNTHETIC_SAMPLES
Extend X by SYNTHETIC_SAMPLES

Adaptive synthetic sampling approach (ADASYN) Text mostly based on He et al., 2010

Adaptive synthetic sampling approach (ADASYN) is a sampling approach for learning from imbalanced datasets. The main idea is to use a weighted distribution for different minority class examples according to their level of difficulty in learning, where more synthetic data is generated for minority class examples that are harder to learn compared to those minority examples that are easier to learn. Thus, ADASYN improves learning with respect to the data distributions by reducing the bias introduced by the class imbalance and by adaptively shifting the classification boundary toward the difficult examples.

The objectives of ADASYN are reducing bias and learning adaptively. The key idea of this algorithm is to use a density distribution as a criterion to decide the number of synthetic samples that need to be generated for each minority data example. Physically, this density distribution is a distribution of weights for different minority class examples according to their level of difficulty in learning. The resulting dataset after using ADASYN will not only provide a balanced representation of the data distribution (according to the desired balance level defined in the configuration), but it also forces the learning algorithm to focus on those difficult to learn examples. It has been shown He et al., 2010, that this algorithm improves accuracy for both minority and majority classes and does not sacrifice one class in preference for another.

ADASYN is not limited to only two-class learning, but can also be generalized to multiple-class imbalanced learning problems as well as incremental learning applications.

For more details and comparisons of ADASYN to other algorithms, please see He et al., 2010.

Existing implementations

Imbalanced-learn is an open-source Python library which provides a suite of algorithms for treating the class imbalance problem.

For augmentig image data, one can use of of the following:

  • Albumentations
  • ImgAug
  • Autoaugment
  • Augmentor
  • DeepAugmnent

But it is also possible to use tools directly implemented by tensorflow, keras etc. For example:

flipped_image = tf.image.flip_left_right(image)

Deep Learning-based SDA Techniques

In data science, data augmentation techniques are used to increase the amount of data by either synthetically creating data from already existing samples via a GAN or modifying the data at hand with small noise or rotation. (Rebuffi et al., 2021)

More recently, data augmentation studies have begun to focus on the field of deep learning (DL), more specifically on the ability of generative models, like Generative Adversarial Networks (GANs) and Variational Autoencoders (VAEs), to create artificial data. This synthetic data is then introduced during the classification model training process to improve performance and results.

Generative Adversarial Networks (GANs) The following text is written based on the works by Musella & Pandolfi, 2018 and Hashemi et al., 2019 and Kansal et al., 2022 and Rehm et al., 2021 and Choi & Lim, 2021 and Kansal et al., 2020

GANs have been proposed as a fast and accurate way of modeling high energy jet formation (Paganini et al., 2017a) and modeling showers throughcalorimeters of high-energy physics experiments (Paganini et al., 2017 ; Paganini et al., 2012; Erdman et al., 2020; Musella & Pandolfi, 2018) GANs have also been trained to accurately approximate bottlenecks in computationally expensive simulations of particle physics experiments. Applications in the context of present and proposed CERN experiments have demonstrated the potential of these methods for accelerating simulation and/or improving simulation fidelity (ATLAS Collaboration, 2018; SHiP Collaboration, 2019).

The generative model approximates the combined response of aparticle detecor simulation and reconstruction algorithms to hadronic jets given the latent space of uniformly distributed noise, auxiliary features and jet image at particle level (jets clustered from the list of stable particles produced by PYTHIA).

In the paper by Musella & Pandolfi, 2018, the authors apply generative models parametrized by neural networks (GANs in particular) to the simulation of particles-detector response to hadronic jets. They show that this parametrization achieves high-fidelity while increasing the processing speed by several orders of magnitude.

Their model is trained to be capable of predicting the combined effect of particle-detector simulation models and reconstruction algorithms to hadronic jets.

Generative adversarial networks (GANs) are pairs of neural networks, a generative and a discriminative one, that are trained concurrently as players of a minimax game (Musella & Pandolfi, 2018). The task of the generative network is to produce, starting from a latent space with a fixed distribution, samples that the discriminative model tries to distinguish from samples drawn from a target dataset. This kind of setup allows the distribution of the target dataset to be learned, provided that both of the networks have high enough capacity.

The input to these networks are hadronic jets, represented as "gray-scale" images of fixed size centered around the jet axis, with the pixel intensity corresponding to the energy fraction in a given cell. The architectures of the networks are based on the image-to-image translation. There few differences between this approach and image-to-image translation. Firstly, non-empty pixels are explicitly modelled in the generated images since these are much sparser than the natural ones. Secondly, feature matching and a dedicated adversarial classifier enforce good modelling of the total pixel intensity (energy). Lastly, the generator is conditioned on some auxiliary inputs.

By predicting directly the objects used at analysis level and thus reproducing the output of both detector simulation and reconstruction algorithms, computation time is reduced. This kind of philosophy is very similar to parametrized detector simulations, which are used in HEP for phenomenological studies. The attained accuracies are comparable to the full simulation and reconstruction chain.

Variational autoencoders (VAEs)

The following section is partly based on Otten et al., 2021

In contrast to the traditional autoencoder (AE) that outputs a single value for each encoding dimension, variational autoencoders (VAEs) provide a probabilistic interpretation for describing an observation in latent space.

In case of VAEs, the encoder model is sometimes referred to as the recognition model and the decoder model as generative model.

By constructing the encoder model to output a distribution of the values from which we randomly sample to feed into our decoder model, we are enforcing a continuous, smooth latent space representation. Thus we expect our decoder model to be able to accurately reconstruct the input for any sampling of the latent distributions, which then means that values residing close to each other in latent space should have very similar reconstructions.

ML-powered Data Generation for Fast Simulation

The following text is based on this Chen et al., 2020

We rely on accurate simulation of physics processes, however currently it is very common for LHC physics to be affected by large systematic uncertanties due to the limited amount of simulated data, especially for precise measurements of SM processes for which large datasets are already available. So far the most widely used simulator is GEANT4 that provides state-of-the-art accuracy. But running this is demanding, both in terms of time and resources. Consequently, delivering synthetic data at the pace at which LHC delivers real data is one of the most challenging tasks for computing infrastructures of the LHC experiments. The typical time it takes to simulate one single event is in the ballpark of 100 seconds.

Recently, generative algorithms based on deep learning have been proposed as a possible solution to speed up GEANT4. However, one needs to work beyond the collision-as-image paradigm so that the DL-based simulation accounts for the irregular geometry of a typical detector while delivering a dataset in a format compatible with downstream reconstruction software.

One method to solve this bottleneck was proposed by Chen et al., 2020. They adopt a generative DL model to convert an analysis specific representation of collision events at generator level to the corresponding representation at reconstruction level. Thus, this novel, fast-simulation workflow starts from a large amount of generator-level events to deliver large analysis-specific samples.

They trained a neural network to model detector resolution effects as a transfer function acting on an analysis-specific set of relevant features, computed at generator level. However, their model does not sample events from a latent space (like a GAN or a plain VAE). Instead, it works as a fast simulator of a given generator-level event, preserving the correspondence between the reconstructed and the generated event, which allows us to compare event-by-event residual distributions. Furthermore, this model is much simpler than a generative model.

Step one in this workflow is generating events in their full format, which is the most resource heavy task, where, as noted before, generating one event takes roughly 100 seconds. However, with this new proposed method O(1000) events are generated per second. This would save on storage: for the full format O(1) MB/event is needed, where for the DL model only 8 MB was used to store 100000 events. To train the model, they used NVIDIA RTX2080 and it trained for 30 minutes, which in terms of overall production time is negligible. For generating N=1M events and n=10%N, one would save 90% of the CPU resources and 79% of the disk storage. Thus augmenting the centrally produced data is a viable method and could help the HEP community to face the computing challenges of the High-Luminosity LHC.

Another more extreme approach investigated the use of GANs and VAEs for generating physics quantities which are relevant to a specific analysis. In this case, one learns the N-dimensional density function of the event, in a space defined by the quantities of interest for a given analysis. So sampling from this function, one can generate new data. Trade-off between statistical precision (decreases with the increasing amount of generated events) and the systematic uncertainty that could be induced by a non accurate description of the n-dim pdf.

Qualitatively, no accuracy deterioration was observed due to scaling the dataset size for DL. This fact proves the robustness of the proposed methodology and its effectiveness for data augmentation.

Open challenges in Data Augmentation

Excerpts are taken from Li, 2020

The limitations of conventional data augmentation approaches reveal huge opportunities for research advances. Below we summarize a few challenges that motivate some of the works in the area of data augmentation.

  • From manual to automated search algorithms: As opposed to performing suboptimal manual search, how can we design learnable algorithms to find augmentation strategies that can outperform human-designed heuristics?
  • From practical to theoretical understanding: Despite the rapid progress of creating various augmentation approaches pragmatically, understanding their benefits remains a mystery because of a lack of analytic tools. How can we theoretically understand various data augmentations used in practice?
  • From coarse-grained to fine-grained model quality assurance: While most existing data augmentation approaches focus on improving the overall performance of a model, it is often imperative to have a finer-grained perspective on critical subpopulations of data. When a model exhibits inconsistent predictions on important subgroups of data, how can we exploit data augmentations to mitigate the performance gap in a prescribed way?

References

Content may be edited and published elsewhere by the author.

Page author: Laurits Tani, 2022