Cross-validation

However, in practice what one often deals with is a hyperparameter optimisation - running of several trainings to find the optimal hyperparameter for a given family of models (e.g. BDT or feed-forward NN).

The number of trials in the hyperparameter space can easily reach hundreds or thousands, and in that case naive approach of training the model for each hyperparameters' set on the same train data set and evaluating its performance on the same test data set is very likely prone to overfitting. In that case, an experimentalist overfits to the test data set by choosing the best value of the metric and effectively adapting the model to suit the test data set best, therefore loosing the model's ability to generalise.

In order to prevent that, a cross-validation (CV) technique is often used:

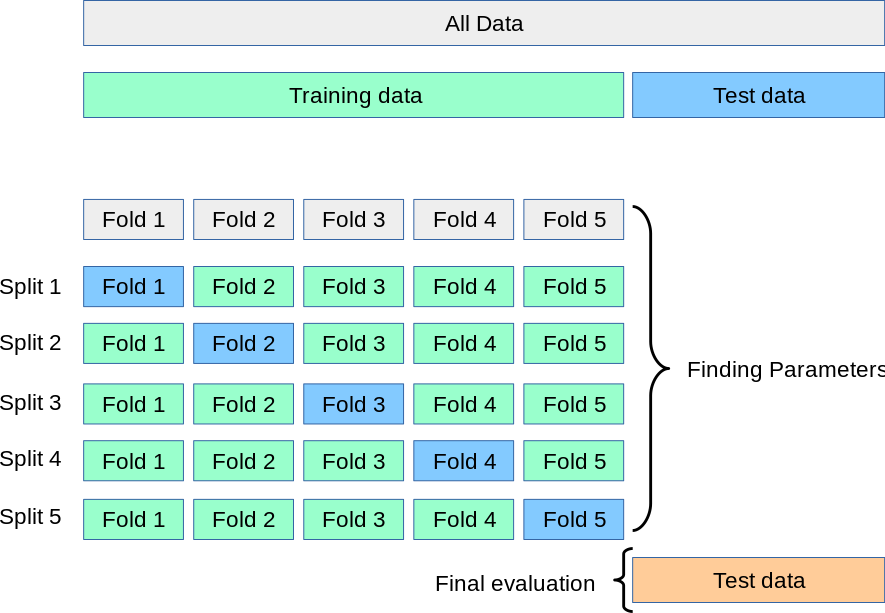
Figure 1. Illustration of the data set split for cross-validation. [source: scikit-learn.org/stable/modules/cross_validation.html]

The idea behind it is that instead of a single split of the data into train/validation sets, the training data set is split into N folds. Then, the model with the same fixed hyperparameter set is trained N times in a way that at the i-th iteration the i-th fold is left out of the training and used only for validation, while the other N-1 folds are used for the training.

In this fashion, after the training of N models in the end there is N values of a metric computed on each fold. The values now can be averaged to give a more robust estimate of model performance for a given hyperparameter set. Also a variance can be computed to estimate the range of metric values. After having completed the N-fold CV training, the same approach is to be repeated for other hyperparameter values and the best set of those is picked based on the best fold-averaged metric value.

Further insights

Effectively, with CV approach the whole training data set plays the role of a validation one, which makes the overfitting to a single chunk of it (as in naive train/val split) less likely to happen. Complementary to that, more training data is used to train a single model oppositely to a single and fixed train/val split, moreover making the model less dependant on the choice of the split.

Alternatively, one can think of this procedure is of building a model ensemble which is inherently an approach more robust to overfitting and in general performing better than a single model.